题目内容
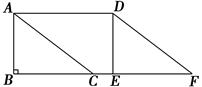
如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.
(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.

(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.

(1)见解析 (2)见解析
解:(1)如图所示:

(2)四边形BFDE的形状是平行四边形,
理由如下:
∵在平行四边形ABCD中,∴∠DAC=∠ACB,AD=BC,
在△ADE和△CBF中,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°﹣∠AED,∠BFE=180°﹣∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形.
(1)作∠CBM=∠ADE,其中BM交CD于F即可;
(2)四边形BFDE的形状是平行四边形,连BE、DF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论.

(2)四边形BFDE的形状是平行四边形,
理由如下:
∵在平行四边形ABCD中,∴∠DAC=∠ACB,AD=BC,
在△ADE和△CBF中,

∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°﹣∠AED,∠BFE=180°﹣∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形.
(1)作∠CBM=∠ADE,其中BM交CD于F即可;
(2)四边形BFDE的形状是平行四边形,连BE、DF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论.

练习册系列答案
相关题目


 ,
, ,则点A′的坐标 .
,则点A′的坐标 .

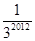



 进行如下操作:先把点
进行如下操作:先把点 ,再把所得数对应的点向右平移1个单位,得到点
,再把所得数对应的点向右平移1个单位,得到点 .点
.点 在数轴上,对线段
在数轴上,对线段 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段 ,其中点
,其中点 .如图1,若点
.如图1,若点 表示的数是
表示的数是 ,则点
,则点 表示的数是 ;若点
表示的数是 ;若点 表示的数是2,则点
表示的数是2,则点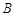 表示的数是 ;已知线段
表示的数是 ;已知线段 经过上述操作后得到的对应点
经过上述操作后得到的对应点 与点
与点
 中,对正方形
中,对正方形 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数
及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数 ,将得到的点先向右平移
,将得到的点先向右平移 个单位,再向上平移
个单位,再向上平移 个单位(
个单位( ),得到正方形
),得到正方形 及其内部的点,其中点
及其内部的点,其中点 。已知正方形
。已知正方形 经过上述操作后得到的对应点
经过上述操作后得到的对应点 与点
与点

 ,﹣
,﹣ ,﹣
,﹣