Question

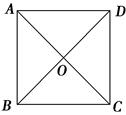
D、E分别是△ABC的边AB、AC的中点．O是平面上的一动点，连接OB、OC，G、F分别是OB、OC的中点，顺次连接点D、E、F、G．
(1)如图1，当点O在△ABC内时，求证：四边形DEFG是平行四边形；
(2)若点O在△ABC外，其余条件不变，点O的位置应满足什么条件，能使四边形DEFG是菱形？请在画2中补全图形，并说明理由．

Answer 1

（1）证明见解析；（2）OA=BC．

试题分析：（1）根据平行四边形的判定性质求证．
（2）把结论当做已知条件，由结论推出已知．
试题解析：（1）∵AB、OB、OC、AC中点分别为D、E、F、G
∴DG、EF分别为△ABC和△OBC的中位线
∴DG∥BC  EF∥BC DG=BC  EF=BC
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形；
（2）当点O满足OA=BC，四边形DEFG是菱形．
由三角形中位线性质得DE=EF，
所以平行四边形DEFG是菱形．