题目内容
【题目】(知识情境)通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
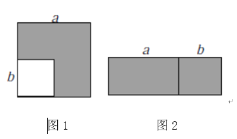
(1)如图1,在边长为![]() 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为![]() 的小正方形
的小正方形![]() .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
.把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
(拓展探究)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
如图3是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.
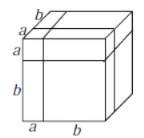
图3
(2)用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
_________________________________________________________________;
(3)已知![]() ,
,![]() ,利用上面的恒等式求
,利用上面的恒等式求![]() 的值.
的值.
【答案】(1)a2-b2=(a+b)(a-b)(2)(a+b)3=a3+3a2b+3ab2+b3(3)40
【解析】
(1)根据平方差公式的几何验证方法即可求解;
(2)根据正方体的体积公式和给出的条件即可得出答案;
(3)根据(2)得出的式子再进行转化,然后把a+b=4,ab=2代入计算即可得出答案.
(1)图1的面积为:a2-b2, 图2的面积为(a+b)(a-b)
∴这个等式是a2-b2=(a+b)(a-b)
故答案为:a2-b2=(a+b)(a-b);
(2)图3的体积为:(a+b)3或a3+3a2b+3ab2+b3
∴这个等式是(a+b)3=a3+3a2b+3ab2+b3
故答案为:(a+b)3=a3+3a2b+3ab2+b3;
(3)由(a+b)3=a3+3a2b+3ab2+b3
得:(a+b)3=a3+3ab(a+b)+b3,
将a+b=4,ab=2代入a3+3ab(a+b)+b3
得:43=a3+3×2×4+b3,
∴a3+b3=6424=40.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案