题目内容
【题目】如图，在平面直角坐标系中，直线 
分别与x轴、y轴交于点B、C，且与直线 
交于点A．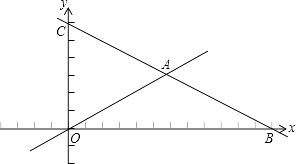
（1）分别求出点A、B、C的坐标；
（2）若D是线段OA上的点，且△COD的面积为12，求直线CD的函数表达式；
（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
【答案】
（1）解：直线 
，
当x=0时，y=6，
当y=0时，x=12，
∴B（12，0），C（0，6），
解方程组：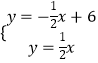 
得： 
，
∴A（6，3），
答：A（6，3），B（12，0），C（0，6）．
（2）解：设D（x， 
x），
∵△COD的面积为12，
∴ ×6×x=12，
解得：x=4，
∴D（4，2），
设直线CD的函数表达式是y=kx+b，把C（0，6），D（4，2）代入得：
，
解得： 
，
∴y=﹣x+6，
答：直线CD的函数表达式是y=﹣x+6．
（3）解：答：存在点Q，如图，
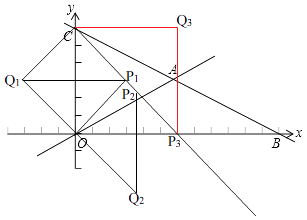
使以O、C、P、Q为顶点的四边形是菱形，点Q的坐标是（6，6）或（﹣3，3）或 
．
【解析】（1）由两函数解析式联立方程，可求出点A的坐标，由直线直线 l 1 的解析式，根据x=0和y=0，建立方程即可求出点B、C的坐标。
（2）已知D是线段OA上的点，可知点D在第一象限，设点D的坐标，根据△COD的面积公式即可求出点D的坐标，再用待定系数法求出直线CD的函数解析式。
（3）要求以O、C、P、Q为顶点的四边形是菱形时，点Q的坐标，分情况讨论，当以OC=6为边时，有两种情况（点Q在第一象限和第四象限）；当以OC为对角线时，根据题意易求出点Q的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对菱形的性质的理解，了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
