题目内容
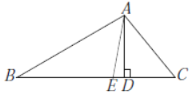
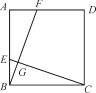
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
【答案】B
【解析】
先连接OA,OB,OC,然后根据三角形的中心的性质和三角形全等判断三个结论的正确性.
连接OA,OB,OC,
因为点O是△ABC的中心,
所以∠AOB=∠BOC=120°,OA=OB=OC
所以∠BOC=∠FOG=120°,∠ABO=∠BCO=30°,
所以∠BOD=∠COE,
所以△BOD≌△COE,
所以OD=OE,结论①正确;
如当E为BC的中点时,S△ODE<S△BDE,所以②错误;因为△BOD≌△COE,所以S△BOD=S△COE,所以S四边形ODBE=S△BOC=![]() S△ABC=
S△ABC=![]() ,结论③正确.
,结论③正确.
故选B

练习册系列答案
相关题目