题目内容
【题目】研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定． 定义：六个内角相等的六边形叫等角六边形．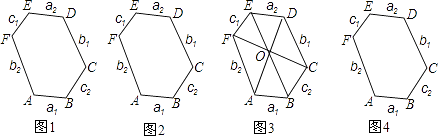
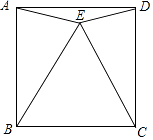
（1）研究性质 ①如图1，等角六边形ABCDEF中，三组正对边AB与DE，BC与EF，CD与AF分别有什么位置关系？证明你的结论．
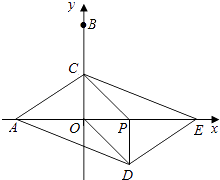
②如图2，等角六边形ABCDEF中，如果有AB=DE，则其余两组正对边BC与EF，CD与AF相等吗？证明你的结论．
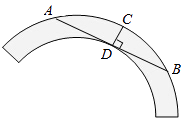
③如图3，等角六边形ABCDEF中，如果三条正对角线AD，BE，CF相交于一点O，那么三组正对边AB与DE，BC与EF，CD与AF分别有什么数量关系？证明你的结论．
（2）探索判定 三组正对边分别平行的六边形，至少需要几个内角为120°，才能保证六边形一定是等角六边形？
【答案】
（1）解：①结论：AB∥DE，BC∥EF，CD∥AF．
证明：连接AD，如图1，
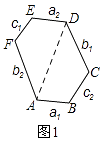
∵六边形ABCDEF是等角六边形，∴∠BAF=∠F=∠E=∠EDC=∠C=∠B= 
=120°．
∵∠DAF+∠F+∠E+∠EDA=360°，∴∠DAF+∠EDA=360°﹣120°﹣120°=120°．
∵∠DAF+∠DAB=120°，∴∠DAB=∠EDA．∴AB∥DE．
同理BC∥EF，CD∥AF．
②结论：EF=BC，AF=DC．
证明：连接AE、DB，如图2，
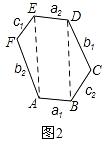
∵AB∥DE，AB=DE，∴四边形ABDE是平行四边形．
∴AE=DB，∠EAB=∠BDE．
∵∠BAF=∠EDC．∴∠FAE=∠CDB．
在△AFE和△DCB中，
．
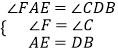∴△AFE≌△DCB．
∴EF=BC，AF=DC．
③结论：AB=DE，AF=DC，EF=BC．
延长FE、CD相交于点P，延长EF、BA相交于点Q，延长DC、AB相交于点S，如图3．
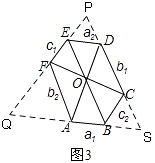
∵六边形ABCDEF是等角六边形，∴∠BAF=∠AFE=120°．∴∠QAF=∠QFA=60°．
∴△QAF是等边三角形．∴∠Q=60°，QA=QF=AF．
同理：∠S=60°，SB=SC=BC；∠P=60°，PE=PD=ED．
∵∠S=∠P=60°，∴△PSQ是等边三角形．∴PQ=QS=SP．
∴QB=QS﹣BS=PS﹣CS=PC．∴AB+AF=AB+QA=QB=PC=PD+DC=ED+DC．
∵AB∥ED，∴△AOB～△DOE．∴ 
．
同理： 
， 
．
∴ 
．
∴ = 
=1．
∴AB=ED，AF=DC，EF=BC．
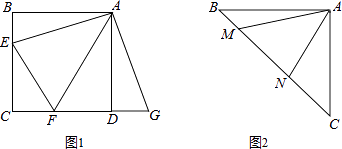
（2）解：连接BF，如图4，
∵BC∥EF，∴∠CBF+∠EFB=180°．
∵∠A+∠ABF+∠AFB=180°，∴∠ABC+∠A+∠AFE=360°．
同理：∠A+∠ABC+∠C=360°．
∴∠AFE=∠C．
同理：∠A=∠D，∠ABC=∠E．
Ⅰ．若有2个内角等于120°，不能保证该六边形一定是等角六边形．
反例：当∠A=∠D=120°，∠ABC=150°时，∠E=∠ABC=150°．
∵六边形的内角和为720°，∴∠AFE=∠C= 
（720°﹣120°﹣120°﹣150°﹣150°）=90°．
此时该六边形不是等角六边形．
Ⅱ．若有3个内角等于120°，能保证该六边形一定是等角六边形．
设∠A=∠D=α，∠ABC=∠E=β，∠AFE=∠C=γ．则2α+2β+2γ=720°．∴α+β+γ=360°．
∵有3个内角等于120°，∴α、β、γ中至少有两个为120°．
若α、β、γ都等于120°，则六个内角都等于120°；
若α、β、γ中有两个为120°，根据α+β+γ=360°可得第三个也等于120°，则六个内角都等于120°．
综上所述：至少有3个内角等于120°，能保证该六边形一定是等角六边形．
【解析】（1）通过验证容易得到猜想：三组正对边分别平行．要证明两条线段平行，只需证明同位角相等或内错角相等或同旁内角互补，要证AB∥DE，只需连接AD，证明∠ADE=∠DAB即可，其它两组同理可得．（2）要证BC=EF，CD=AF，只需连接AE、BD，证明△AFE≌△DCB即可．（3）由条件“三条正对角线AD，BE，CF相交于一点O”及（1）中的结论可证到 = ，将等角六边形ABCDEF补成等边三角形后，可以证到AB+AF=DE+DC，从而得到三组正对边分别相等．（4）若只有1个内角为120°或有2个内角为120°，可以通过举反例说明该六边形不一定是等角六边形；若有3个内角为120°，可以通过分类讨论证明该六边形一定是等角六边形．
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°，以及对平行四边形的判定与性质的理解，了解若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．
