题目内容
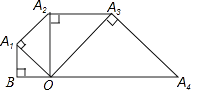
【题目】如图，△ABC中，AB=4，AC=2，BC=2 
，以BC为直径的半圆交AB于点D，以A为圆心，AC为半径的扇形交AB于点E． 
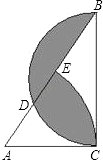
（1）以BC为直径的圆与AC所在的直线有何位置关系？请说明理由；
（2）求图中阴影部分的面积（结果可保留根号和π）．
【答案】
（1）解：相切．
理由：∵22+（2 
）2=16=42，
∴AC2+BC2=AB2．
∴∠ACB=90°．
∴以BC为直径的圆与AC所在的直线相切
（2）解：∵Rt△ABC中，cosA= 
= 
．
∴∠A=60°．
∴S阴影=S半圆﹣（S△ABC﹣S扇形ACE）
= π（ ）2﹣（ ×2×2 ﹣ 
π×22）= 
﹣2
【解析】（1）根据切线的判定定理，证明∠ACB=90°即可；（2）根据S阴影=S半圆﹣（S△ABC﹣S扇形ACE），即可求解．
【考点精析】本题主要考查了三角形的面积和直线与圆的三种位置关系的相关知识点，需要掌握三角形的面积=1/2×底×高；直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．
【题目】某校为了选拔学生参加“汉字听写大赛”，对九年级一班、二班各10名学生进行汉字听写测试．计分采用10分制（得分均取整数），成绩达到6分或6分以上为及格，得到9分为优秀，成绩如表1所示，并制作了成绩分析表（表2）． 表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
（1）在表2中，a= ， b=；
（2）有人说二班的及格率、优秀率均高于一班，所以二班比一班好；但也有人认为一班成绩比二班好，请你给出坚持一班成绩好的两条理由；
（3）一班、二班获满分的中同学性别分别是1男1女、2男1女，现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”，用树状图或列表法求出恰好抽到1男1女两位同学的概率．
【题目】抛物线y=ax+bx+c上部分点的横坐标x，纵坐标y的对应值如下表，从下表可知：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
下列说法错误的是（ ）。
A.抛物线与x轴的另一个交点为（3，0）；
B.函数的最大值为6；
C.抛物线的对称轴是直线x=0.5；
D.在对称轴的左侧，y随x的增大而增大。
