题目内容
【题目】在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )
A.DE∥BC
B.∠AED=∠B
C.AE:AD=AB:AC
D.AE:DE=AC:BC
【答案】D
【解析】解:如图, 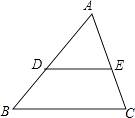
A、∵DE∥BC,
∴△ADE∽△ABC,故本选项错误;
B、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故本选项错误;
C、∵AE:AD=AB:AC,∠A=∠A,
∴△ADE∽△ACB,故本选项错误;
D、AE:DE=AC:BC不能使△ADE和△ABC相似,故本选项正确.
故选D.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
相关题目