题目内容
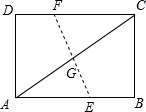
将一张边长分别为8、6的矩形纸片ABCD折叠，使点C与点A重合，则折痕的长为（ ）
| A．6 | B．6.5 | C．7.5 | D．10 |
如图，设折痕EF与对角线AC的交点为G，则AC⊥EF，
即∠AGE=90°，
∵四边形ABCD是矩形，
∴∠B=90°，
∴∠AGE=∠B，
又∵∠GAE=∠BAC，
∴△AGE∽△ABC，
∴AG：AB=EG：BC，
∵AB=8，BC=6，
∴AC=
=10，
由折叠的性质可得：AG=
AC=5，
∴EG=
=
=
，
∵AB∥CD，
∴△AGE∽△CGF，
∴AG：CG=EG：FG，
∴FG=EG=
，
∴EF=FG+EG=7.5．
故选C．
即∠AGE=90°，
∵四边形ABCD是矩形，
∴∠B=90°，
∴∠AGE=∠B，
又∵∠GAE=∠BAC，
∴△AGE∽△ABC，
∴AG：AB=EG：BC，
∵AB=8，BC=6，
∴AC=
| AB2+BC2 |
由折叠的性质可得：AG=
| 1 |
| 2 |
∴EG=
| AG•BC |
| AB |
| 5×6 |
| 8 |
| 15 |
| 4 |
∵AB∥CD，
∴△AGE∽△CGF，
∴AG：CG=EG：FG，
∴FG=EG=
| 15 |
| 4 |
∴EF=FG+EG=7.5．
故选C．
练习册系列答案
相关题目
C上的两点，E，G分别是折痕CE，AG与AB，CD的交点．
