题目内容
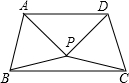
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为( )


| A.1 | B.2
| C.2
| D.12 |
∵菱形AECF,AB=6,
∴假设BE=x,
∴AE=6-x,
∴CE=6-x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=6-x,
解得:x=2,
∴CE=4,利用勾股定理得出:
BC2+BE2=EC2,
BC=
=
=2
,
故选:C.

∴假设BE=x,
∴AE=6-x,
∴CE=6-x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=6-x,
解得:x=2,
∴CE=4,利用勾股定理得出:
BC2+BE2=EC2,
BC=
| EC2-BE2 |
| 42-22 |
| 3 |
故选:C.

练习册系列答案
相关题目