Question

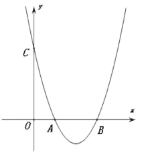
【题目】如图所示，抛物线与轴交于两点，，与轴交于，并且对称轴．

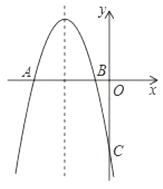
（1）求抛物线的解析式；

（2）在轴上方的抛物线上，过的直线与直线交于点，与轴交于点，求的最大值；

（3）点为抛物线对称轴上一点，当是以为直角边的直角三角形时，求点坐标；

Answer 1

【答案】（1）；（2）的最大值为；（3）点的坐标为或．

【解析】

（1）利用待定系数法求解可得；

（2）先求AC解析式，作PH∥y轴交AC于H，作PG⊥y轴，设出P的坐标，，由MN的解析式的特点判断，利用三角函数把PM，PN的长度转化到PH，PG的上，利用及二次函数的性质进一步求解可得；

（3）设D（-3，y），利用两点间的距离公式得到 ，然后分类：当△ACD是以AC为直角边、CD为斜边和以AC为直角边、AD为斜边的直角三角形时，分别解方程求出y即可得到对应的D点坐标；

解：（1）∵抛物线过，对称轴为直线，∴点坐标为，

可设抛物线解析式为，将点代入，得：，

解得，则抛物线解析式为；

（2）设点坐标为，

∴直线解析式为，

过点作轴交于，作轴于，

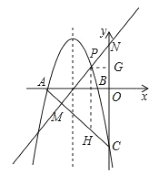
的解析式为，

，

，

，

的最大值为；

（3）①设，

则，

当是以为直角边、为斜边的直角三角形时，

，即，

解得，此时；

当是以为直角边、为斜边的直角三角形时，

，即，

解得，此时点；

综上，点的坐标为或．