题目内容
【题目】在学习一元一次方程的解法时，我们经常遇到这样的试题：
“解方程：
”，请根据解题过程，在后面的括号内写出变形依据．
解：去分母，得 （ ）
去括号，得 （ ）
移项，得 （ ）
合并，得 （合并同类项法则）
系数化为 1，得 （ ）
请你写出在进行运算时容易出错的地方（至少写出三个）．
【答案】答案见解析
【解析】
（1）方程去分母，去括号，移项合并，把x系数化为1，求出解；
（2）提出三条运算时容易出错的地方即可．
（1）去分母，得：15x﹣3（x﹣2）＝5（2x﹣5）﹣45（等式的性质）
去括号，得：15x﹣3x+6＝10x﹣25﹣45（去括号法则）
移项，得：15x﹣3x﹣10x＝﹣25﹣45﹣6（等式的性质）
合并，得：2x＝﹣76（合并同类项）
系数化为1，得：x＝﹣38（等式的性质）；
（2）去分母时各项都要乘以15；去括号时，括号外边是负号时注意变号；移项时注意要变号．
故答案为：（1）15x﹣3（x﹣2）＝5（2x﹣5）﹣45；等式的性质；15x﹣3x+6＝10x﹣25﹣45；去括号法则；15x﹣3x﹣10x＝﹣25﹣45﹣6；等式的性质；2x＝﹣76；x＝﹣38；等式的性质．
【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项，下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄（岁）： 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据，解答下列问题：
小彬按“组距为5”列出了如图的频数分布表
分组 | 频数 |
A：25～30 | |
B：30～35 | 15 |
C：35～40 | 31 |
D：40～45 | |
合计 | 56 |
（1）每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图；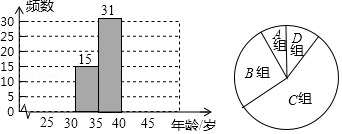 
（2）根据（1）中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征；
（3）在（1）的基础上，小彬又画了如图所示的扇形统计图，图中获奖年龄在30～35岁的人数约占获奖总人数的%（百分号前保留1位小数）；C组所在扇形对应的圆心角度数约为°（保留整数）
