题目内容
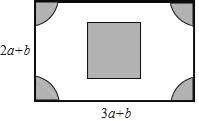
【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为![]() .
.

(1)图①中打包带的总长![]() =________.
=________.
图②中打包带的总长![]() =________.
=________.
(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较 ![]() 的大小.)
的大小.)
(3)若b=40且a为正整数,在数轴上表示数![]() 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
【答案】(1)l=4a+2b+180,l=2a+4b+180;(2)第2种,l- l=2(a-b),理由见解析;
(3)a=50
【解析】
(1)根据图形,不难看出:图①打包带的长有长方体的四个长、两个宽、六个高,图②打包带的长有长方体的两个长、四个宽、六个高,从而可以解答本题;
(2)根据(1)中的答案可以求得哪一种打包方式更节省材料;
(3)根据(2)中的关系式,代入b的值,再根据![]() 的两点之间有且只有19个整数点即可求解.
的两点之间有且只有19个整数点即可求解.
解:(1)图①四个长为4a,两个宽为2b,六个高为30×6=180,
∴打包带的长l=4a+2b+180,
图②两个长为2a,四个宽为4b,六个高为30×6=180,
∴打包带的长l=2a+4b+180,
故答案为l=4a+2b+180,l=2a+4b+180.
(2)第2种打包方式更节省材料,理由如下:
(4a+2b+180)-(2a+4b+180),
=4a+2b+180-2a-4b-180,
=2(a-b),
∵![]() ,
,
∴2(a-b)>0,
∴第2种打包方式更节省材料;
(3)当![]() 时, 2(a-b)=2(a-40) =2a-80,
时, 2(a-b)=2(a-40) =2a-80,
∵在数轴上表示数![]() 的两点之间有且只有19个整数点, 且
的两点之间有且只有19个整数点, 且![]() 为正整数,
为正整数,
∴a=50.

 阅读快车系列答案
阅读快车系列答案