题目内容
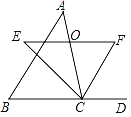
【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

【答案】(1)见解析;(2) EF⊥AE仍成立,理由见解析.
【解析】
(1)如图1,先根据三角形内角和定理得出∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,由∠B=∠C,∠AEB=∠CEF,得到∠BAE=∠EFC,再由角平分线定义得出∠BAE=∠DAE,等量代换得到∠EFC=∠DAE.由平角的定义得出∠EFC+∠EFD=180°,那么∠DAE+∠EFD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,进而得到∠AEF=90°,由垂直的定义证明出EF⊥AE;
(2)如图2,先根据三角形外角的性质得出∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,由∠ABC=∠BCD,∠AEB=∠CEF,得到∠1=∠F,再由角平分线定义得出∠1=∠2,等量代换得到∠F=∠2.由平角的定义得出∠2+∠EAD=180°,那么∠F+∠EAD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠F+∠EAD)=180°,进而得到∠AEF=90°,由垂直的定义得出EF⊥AE.
(1)证明:如图1,∵∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,
∠B=∠C,∠AEB=∠CEF,
∴∠BAE=∠EFC,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠EFC=∠DAE.
∵∠EFC+∠EFD=180°,
∴∠DAE+∠EFD=180°,
∴∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE;
(2)解:如图2,若AE平分∠BAD的外角,其余条件不变,(1)中结论没有变化.理由如下:
∵∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,
∠ABC=∠BCD,∠AEB=∠CEF,
∴∠1=∠F,
∵AE平分∠BAD的外角,
∴∠1=∠2,
∴∠F=∠2.
∵∠2+∠EAD=180°,
∴∠F+∠EAD=180°,
∴∠AEF+∠D=360°-(∠F+∠EAD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE.