题目内容
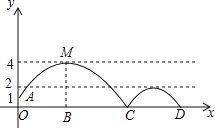
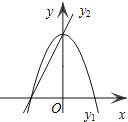
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.那么使得M=1的x值为______.
【答案】![]() 或
或![]()
【解析】
利用图象与坐标轴交点以及M值的取法,分别利用图象进行分析即可得出答案.
解:如图,
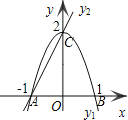
∵y1=-2x2+2,
∴抛物线与坐标轴的交点是:(-1,0),(1,0),(0,2).
∵直线y2=2x+2,
∴该直线与坐标轴的交点是:(-1,0),(0,2).
即A(-1,0),B(1,0),C(0,2).
根据图示知,①当-1<x<0时,y1>y2,
∴使得M=1时,y2=2x+2=1,解得:x=-![]() ;
;
②当x>0时,y2>y1,
使得M=1时,即y1=-2x2+2=1,解得:x1=![]() ,x2=-
,x2=-![]() (舍去),
(舍去),
∴使得M=1的x值是-![]() 或
或![]() .
.
故答案是:-![]() 或
或![]() .
.

练习册系列答案
相关题目