题目内容
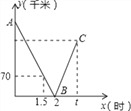
【题目】甲、乙两车同时从A地出发,沿同一条笔直的公路匀速前往相距360km的B地,半小时后甲发现有东西落在A地,于是立即以原速返回A地取物品,取到物品后立即以比原来速度每小时快15km继续前往B地(所有掉头时问和领取物品的时问忽略不计),甲、乙两车之间的距离y(km)与甲车行驶的时间x(h)之问的部分函数关系如图所示:当甲车到达B地时,乙车离B地的距离是多少.
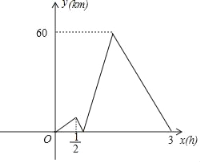
【答案】乙车离B地距离为60千米.
【解析】
先求出乙的速度,再列方程求出甲重新出发后的速度,然后计算出甲行走的总时间,可得此时乙行驶的路程,然后可得结果.
∵甲出发到返回用时0.5小时,返回后速度不变,
∴返回到A地的时刻为x=1,此时y=60,
∴乙的速度为60千米/时.
设甲重新出发后的速度为v千米/时,列得方程:
(3﹣1)(v﹣60)=60,
解得:v=90.
设甲在第t分钟到达B地,列得方程:
90(t﹣1)=360,
解得:t=5.
∴此时乙行驶的路程为:60×5=300(千米).
离B地距离为:360﹣300=60(千米).

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目