题目内容
【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


【答案】该塔AC的高度约80m.
【解析】分析:延长DF交AC于点G,设AG=xm,根据正切的概念用x表示出DG和FG,根据图形列出方程求出x的值,计算即可.
详解:延长DF交AC于点G,
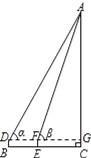
设AG=xm.由题意知:DF=13.1 m,DB=FE=GC=1.4 m.
在Rt△ADG中,tan∠ADG=![]() ,∴DG=
,∴DG=![]() =
=![]() ≈
≈![]() ,
,
在Rt△AFG中,tan∠AFG=![]() ,∴FG=
,∴FG=![]() =
=![]() ≈
≈![]() ,
,
∵DF=DG﹣FG,∴![]() =13.1,解得x=78.6,∴AG=78.6 m,
=13.1,解得x=78.6,∴AG=78.6 m,
∵AC=AG+GC,∴AC=78.6+1.4=80(m).
答:该塔AC的高度约80m.

练习册系列答案
相关题目