题目内容
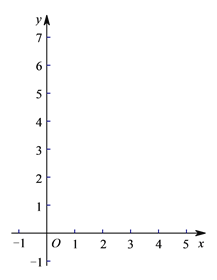
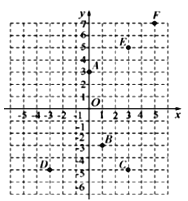
【题目】（1）在如图所示的平面直角坐标系中表示下面各点：A(0，3)；B(1，－3)；C(3，－5)；D(－3，－5)；E(3，5)；F(5，7)．
①B点到x轴的距离是 ，到y轴的距离是 ．
②将点C向x轴的负方向平移 个单位，它就与点D重合．
③连接CE，则直线CE与y轴是 关系．
（2）一个正方形的面积是15，若它的边长的整数部分为
，小数部分为
，求
的值．
【答案】(1)作图见解析①3，1；②6；③平行；（2）6.
【解析】
（1）在坐标平面内作出各点即可.
①根据点到坐标轴的距离计算方法求解即可；
②根据平移规律：向左平移6个单位，继而即可得出答案；
③点C和点E的横坐标相等，可知直线CE与y轴平行；
（2）求出正方形的边长为
，估算出a和b的值，代入求值即可.
（1）在平面直角坐标系中表示出各点，如下所示：
①B点坐标为（1，-3），
故B点到x轴的距离是3，到y轴的距离是1；
②将点C向左平移6个单位后与点D重合；
③∵点C和点E的横坐标相等，
∴直线CE与y轴平行；
（2）∵一个正方形的面积为15，
∴正方形的边长为，
∵3<<4
∴a=3，b=-3
∴
=32+-3-=6.
练习册系列答案
相关题目
【题目】“春种一粒粟，秋收万颗子”，唐代诗人李绅这句诗中的“粟”即谷子（去皮后则称为“小米”），被誉为中华民族的哺育作物．我省有着“小杂粮王国”的美誉，谷子是我省杂粮谷物中的大类．某小米经销商要将规格相同的1000袋小米运往
，
，
三地销售，要求运往地的袋数是运往地袋数的3倍，各地的运费如下表所示：
运往地 |
|
|
|
运费（元/袋） | 20 | 10 | 15 |
（1）设运往地的小米为
（袋），总运费为
（元），试写出与的函数关系式；
（2）若总运费不超过14000元，最多可运往地多少袋小米？
