题目内容
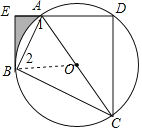
【题目】如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为4,请求出图中阴影部分的面积.

【答案】(1)BE与⊙O相切,证明见解析;(2)![]() π.
π.
【解析】试题分析:(1)连接BO,根据等腰三角形的性质得到∠1=∠2,根据角平分线的定义得到![]() 等量代换得到
等量代换得到![]() 根据余角的性质得到
根据余角的性质得到![]() 于是得到结论;
于是得到结论;
(2)根据已知条件得到![]() 是等边三角形,得到
是等边三角形,得到![]() 解直角三角形得到
解直角三角形得到![]() 于是得到结论.
于是得到结论.
试题解析:(1)BE与![]() 相切,
相切,
理由:连接BO,
∵OA=OB,
∴∠1=∠2,
∵AB平分∠CAE,
∴∠1=∠BAE,
∴∠2=∠BAE,
∵BE⊥AD,
![]()
![]()
![]() 即
即![]()
∴BE⊥OB,
∴BE与![]() 相切;
相切;
![]()
![]()
∵OA=OB,
∴△ABO是等边三角形,
![]()
![]()
在Rt△ABE中, ![]()
![]()
![]()
∴S阴影=S四边形AEBOS扇形AOB=![]()

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目






