题目内容
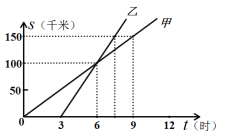
【题目】如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,___________ 是自变量,___________ 是因变量.
(2)甲的速度 ___________ 乙的速度.(填“大于”、“等于”、或“小于”)
(3)甲与乙 ___________ 时相遇.
(4)甲比乙先走 ___________ 小时.
(5)9时甲在乙的 ___________ (填“前面”、“后面”、“相同位置”).
(6)路程为150km,甲行驶了___________ 小时,乙行驶了___________ 小时.
【答案】(1)时间、路程;(2)小于;(3)6;(4)3;(5)后面;(6)9、4.5.
【解析】(1)根据自变量与因变量的含义得到时间是自变量,路程是因变量;
(2)甲走6行驶100千米,乙走3小时行驶了100千米,则可得到它们的速度的大小;
(3)6时两图象相交,说明他们相遇;
(4)观察图象得到甲先出发3小时后,乙才开始出发;
(5)观察图象得到t=9时,乙的图象在甲的上方,即乙行驶的路程远些;
(6)观察图象得到路程为150km,甲行驶9小时;乙行驶了150÷![]() =4.5小时.
=4.5小时.
(1)函数图象反映路程随时间变化的图象,则时间是自变量,路程为因变量;
(2)甲的速度=![]() 千米/时,乙的速度=
千米/时,乙的速度=![]() 千米/时,所以甲的速度小于乙的速度;
千米/时,所以甲的速度小于乙的速度;
(3)6时表示他们相遇,即乙追赶上了甲;
(4)甲先出发3小时后,乙才开始出发;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面
(6)路程为150km,甲行驶9小时;乙行驶了150÷![]() =4.5小时.
=4.5小时.
故答案为:(1)时间、路程;(2)小于;(3)6;(4)3;(5)后面;(6)9、4.5.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为()
A. 4个 B. 3个 C. 2个 D. 1个
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.



