题目内容
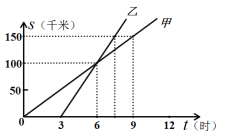
【题目】甲、乙两车同时从A地出发,匀速开往B地.甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动;当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h.设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.
(1)A、B两地的距离是______km,乙车的速度是______km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距150km时,直接写出x的值.

【答案】(1)600,75;(2)线段MN所表示的y与x之间的函数表达式是y=-225x+1200(4≤x≤![]() );(3)2、
);(3)2、![]() 或6.
或6.
【解析】
(1)根据题意和函数图象中的数据可以求得A、B两地的距离和乙车的速度;
(2)根据题意可以写出点M的实际意义,并求得线段MN所表示的y与x之间的函数表达式;
(3)根据题意可以求得各段对应的函数解析式,从而可以解答本题.
解:(1)A、B两地的距离是:150×(8÷2)=600km,
乙车的速度为:600÷8=75km/h,
故答案为:600,75;
(2)点M的实际意义是此时甲车到达B地,
点M的坐标为(4,300),
设点N的横坐标为n,则150n+75n=600×2,得n=![]() ,
,
∴点N的坐标为(![]() ,0),
,0),
设线段MN所表示的y与x之间的函数表达式是y=kx+b,
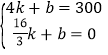 ,得
,得![]() ,
,
即线段MN所表示的y与x之间的函数表达式是y=-225x+1200(4≤x≤![]() );
);
(3)设OM段对应的函数解析式为y=ax,
300=4a,得a=75,
∴OM段对应的函数解析式为y=75x,
令75x=150,得x=2,
∵MN段对应的函数解析式为y=-225x+1200,
∴当-225x+1200=150时,得x=![]() ,
,
设过点N(![]() ,0)、Q(8,600)的函数解析式为y=cx+d,
,0)、Q(8,600)的函数解析式为y=cx+d,
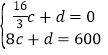 ,得
,得![]() ,
,
即y=225x-1200,
令225x-1200=150,得x=6,
答:当两车相距150km时,x的值是2、![]() 或6.
或6.