题目内容
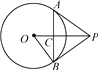
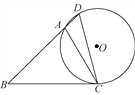
【题目】如图1，在△ACB和△AED中，AC＝BC，AE＝DE，∠ACB＝∠AED＝90°，点E在AB上，F是线段BD的中点，连接CE、FE．
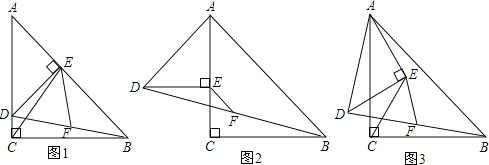
（1）请你探究线段CE与FE之间的数量关系（直接写出结果，不需说明理由）；
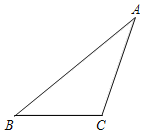
（2）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由；
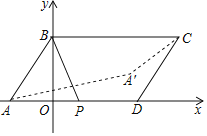
（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由．
【答案】（1）线段CE与FE之间的数量关系是CE＝
FE；（2）（1）中的结论仍然成立．理由见解析；（3）（1）中的结论仍然成立．理由见解析
【解析】
（1）连接CF，直角△DEB中，EF是斜边BD上的中线，因此EF=DF=BF，∠FEB=∠FBE，同理可得出CF=DF=BF，∠FCB=∠FBC，因此CF=EF，由于∠DFE=∠FEB+∠FBE=2∠FBE，同理∠DFC=2∠FBC，因此∠EFC=∠EFD+∠DFC=2（∠EBF+∠CBF）=90°，因此△EFC是等腰直角三角形，CF=EF；
（2）思路同（1）也要通过证明△EFC是等腰直角三角形来求解．连接CF，延长EF交CB于点G，先证△EFC是等腰三角形，可通过证明CF是斜边上的中线来得出此结论，那么就要证明EF=FG，就需要证明△DEF和△FGB全等．这两个三角形中，已知的条件有一组对顶角，DF=FB，只要再得出一组对应角相等即可，我们发现DE∥BC，因此∠EDB=∠CBD，由此构成了两三角形全等的条件．EF=FG，那么也就能得出△CFE是个等腰三角形了，下面证明△CFE是个直角三角形．由上面的全等三角形可得出ED=BG=AD，又由AC=BC，因此CE=CG，∠CEF=45°，在等腰△CFE中，∠CEF=45°，那么这个三角形就是个等腰直角三角形，因此就能得出（1）中的结论了；
（3）思路同（2）通过证明△CFE来得出结论，通过全等三角形来证得CF=FE，取AD的中点M，连接EM，MF，取AB的中点N，连接FN、CN、CF．那么关键就是证明△MEF和△CFN全等，利用三角形的中位线和直角三角形斜边上的中线，我们不难得出EM=PN=
AD，EC=MF=AB，我们只要再证得两对应边的夹角相等即可得出全等的结论．我们知道PN是△ABD的中位线，那么我们不难得出四边形AMPN为平行四边形，那么对角就相等，于是90°+∠CNF=90°+∠MEF，因此∠CNF=∠MEF，那么两三角形就全等了．证明∠CFE是直角的过程与（1）完全相同．那么就能得出△CEF是个等腰直角三角形，于是得出的结论与（1）也相同．
（1）如图1，连接CF，线段CE与FE之间的数量关系是CE＝FE；
解法1：
∵∠AED＝∠ACB＝90°
∴B、C、D、E四点共圆
且BD是该圆的直径，
∵点F是BD的中点，
∴点F是圆心，
∴EF＝CF＝FD＝FB，
∴∠FCB＝∠FBC，∠ECF＝∠CEF，
由圆周角定理得：∠DCE＝∠DBE，
∴∠FCB+∠DCE＝∠FBC+∠DBE＝45°
∴∠ECF＝45°＝∠CEF，
∴△CEF是等腰直角三角形，
∴CE＝EF．
解法2：
易证∠BED＝∠ACB＝90°，
∵点F是BD的中点，
∴CF＝EF＝FB＝FD，
∵∠DFE＝∠ABD+∠BEF，∠ABD＝∠BEF，
∴∠DFE＝2∠ABD，
同理∠CFD＝2∠CBD，
∴∠DFE+∠CFD＝2（∠ABD+∠CBD）＝90°，
即∠CFE＝90°，
∴CE＝EF．
（2）（1）中的结论仍然成立．
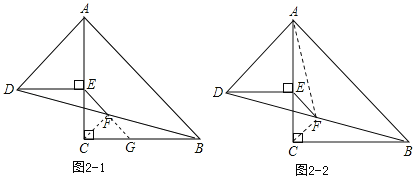
解法1：如图2﹣1，连接CF，延长EF交CB于点G，
∵∠ACB＝∠AED＝90°，
∴DE∥BC，
∴∠EDF＝∠GBF，
又∵∠EFD＝∠GFB，DF＝BF，
∴△EDF≌△GBF，
∴EF＝GF，BG＝DE＝AE，
∵AC＝BC，
∴CE＝CG，
∴∠EFC＝90°，CF＝EF，
∴△CEF为等腰直角三角形，
∴∠CEF＝45°，
∴CE＝FE；
解法2：如图2﹣2，连结CF、AF，
∵∠BAD＝∠BAC+∠DAE＝45°+45°＝90°，
又点F是BD的中点，
∴FA＝FB＝FD，
而AC＝BC，CF＝CF，
∴△ACF≌△BCF，
∴∠ACF＝∠BCF＝∠ACB＝45°，
∵FA＝FB，CA＝CB，
∴CF所在的直线垂直平分线段AB，
同理，EF所在的直线垂直平分线段AD，
又DA⊥BA，
∴EF⊥CF，
∴△CEF为等腰直角三角形，
∴CE＝EF．
（3）（1）中的结论仍然成立．
解法1：如图3﹣1，取AD的中点M，连接EM，MF，取AB的中点N，连接FN、CN、CF，
∵DF＝BF，
∴FM∥AB，且FM＝AB，
∵AE＝DE，∠AED＝90°，
∴AM＝EM，∠AME＝90°，
∵CA＝CB，∠ACB＝90°
∴CN=AN=AB，∠ANC＝90°，
∴MF∥AN，FM＝AN＝CN，
∴四边形MFNA为平行四边形，
∴FN＝AM＝EM，∠AMF＝∠FNA，
∴∠EMF＝∠FNC，
∴△EMF≌△FNC，
∴FE＝CF，∠EFM＝∠FCN，
由MF∥AN，∠ANC＝90°，可得∠CPF＝90°，
∴∠FCN+∠PFC＝90°，
∴∠EFM+∠PFC＝90°，
∴∠EFC＝90°，
∴△CEF为等腰直角三角形，
∴∠CEF＝45°，
∴CE＝FE．
