题目内容
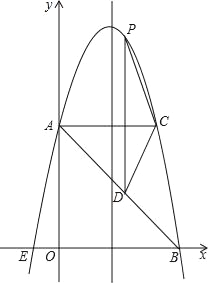
【题目】如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:
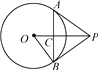
①OP垂直平分AB;
②∠APB=∠BOP;
③△ACP≌△BCP;
④PA=AB;
⑤若∠APB=80°,则∠OBA=40°.
一定正确的是___.
【答案】①③⑤
【解析】由PA、PB是⊙O的两条切线,由切线长定理可得:∠APO=∠BPO,PA=PB,然后由等腰三角形的性质,可得①正确;易证得△ACP≌△BCP;可得③正确,然后由切线的性质,易求得⑤正确.
∵PA、PB是⊙O的两条切线, ∴∠APO=∠BPO,PA=PB,
∴OP垂直平分AB; 故①正确;
∵PB⊥OB,∴∠OBP=90°,∴∠BOP+∠BPO=90°,∴∠BOP+![]() APB=90°,
APB=90°,
得不到∠APB=∠BOP; 故②错误;
在△ACP和△BCP中,PA=PB,PC=PC,AC=BC,∴△ACP≌△BCP;故③正确;
∵PA=PB,但△PAB不一定是等边三角形,∴PA不一定等于AB,故④错误;
∵PA=PB,∴∠PAB=∠PBA,∵∠APB=80°,∴∠ABP=50°,∵∠OBP=90°,
∴∠OBA=40°. ∴正确的是:①③⑤.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目