题目内容
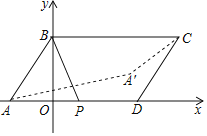
【题目】如图，在平面直角坐标系中，平行四边形ABCD的坐标分别为A（﹣1，0）、B（0，2）、C（4，2）、D（3，0），点P是AD边上的一个动点，若点A关于BP的对称点为A'，则A'C的最小值为（ ）
A.
B.
C.
D.1
【答案】B
【解析】
由轴对称的性质可知BA＝BA′，在△BA′C中由三角形三边关系可知A′C≥BCBA′，则可求得答案．
解：连接BA′，如图：
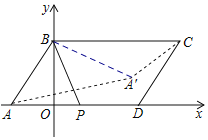
∵平行四边形ABCD的坐标分别为A（﹣1，0）、B（0，2）、C（4，2）、D（3，0），
∴AB＝
，BC＝4，
∵若点A关于BP的对称点为A'，
∴BA′＝BA＝
，
在△BA′C中，由三角形三边关系可知：A′C≥BC﹣BA′，
∴A′C≥4﹣，即A′C的最小值为4﹣，
故选：B．
练习册系列答案
相关题目
