Question

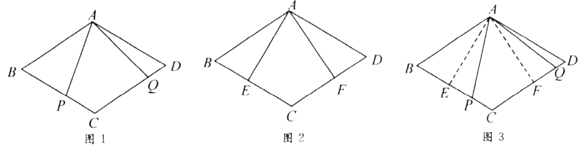
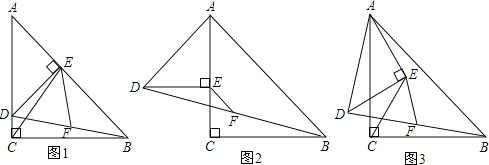
【题目】如图，AD∥BC，∠1＝∠B，∠2＝∠3．

（1）试说明AB∥DE；

（2）AF与DC的位置关系如何；为什么；

（3）若∠B＝68°，∠C＝46°20′，求∠2的度数．

注：本题第（1）、（2）小题在下面的解答过程的空格内填写理由或数学式；第（3）小题要写出解题过程．

解：

（1）∵AD∥BC，（已知）

∴∠1＝∠　． （　　 ）

又∵∠1＝∠B，（已知）

∴∠B＝∠　，（等量代换）

∴　　∥　　． （　　 ）

（2）AF与DC的位置关系是：　　．理由如下：

∵AB∥DE，（已知）

∴∠2＝∠　　． （　　 ）

又∵∠2＝∠3，（已知）

∴∠　　＝∠　　．（等量代换）

∴　∥　　． （　　 ）

Answer 1

【答案】（1）DEC；两直线平行，内错角相等；DEC；AB；DE；同位角相等，两直线平行；（2）AF∥DC；AGD；两直线平行，内错角相等；3；AGD；AF；DC；内错角相等，两直线平行；（3）65°40′．

【解析】

根据平行线的判定和性质解答即可．

（1）∵AD∥BC，（ 已知 ）

∴∠1＝∠DEC．（两直线平行，内错角相等 ）

又∵∠1＝∠B，（ 已知 ）

∴∠B＝∠DEC，（ 等量代换 ）

∴AB∥DE．（ 同位角相等，两直线平行）

（2）AF与DC的位置关系是：AF∥DC．

∵AB∥DE，（ 已知 ）

∴∠2＝∠AGD．（ 两直线平行，内错角相等 ）

又∵∠2＝∠3，（ 已知 ）

∴∠3＝∠AGD，（ 等量代换）

∴AF∥DC．（ 内错角相等，两直线平行 ）

（3）∵AF∥DC，

∴∠AFB＝∠C．

∵AD∥BC，

∴∠AFB＝∠DAF，∠BAD+∠B＝180°．

∴∠2+∠C+∠B＝180°．

又∵∠B＝68°，∠C＝46°20′，

∴∠2＝65°40′．

故答案为：（1）DEC；两直线平行，内错角相等；DEC；AB；DE；同位角相等，两直线平行；（2）AF∥DC；AGD；两直线平行，内错角相等；3；AGD；AF；DC；内错角相等，两直线平行．