题目内容
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3![]() ,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
【答案】(1)3+![]() ;(2)2.
;(2)2.
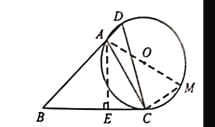
【解析】试题(1)过点A作AE⊥BC,垂足为E,在Rt△ABE和在Rt△ACE中,利用特殊角的三角函数值可分别求出BE=AE=3,EC=![]() ,可得BC=BE+EC=3+
,可得BC=BE+EC=3+![]() ;(2)连接AO并延长到⊙O上一点M,连接CM,在Rt△ACE中,利用∠M=60°,AC=2
;(2)连接AO并延长到⊙O上一点M,连接CM,在Rt△ACE中,利用∠M=60°,AC=2![]() ,可求AM=4,从而得半径是2.
,可求AM=4,从而得半径是2.
试题解析:解:(1)过点A作AE⊥BC,垂足为E,
∴∠AEB=∠AEC=90°,在Rt△ABE中,∵sinB=![]() ,
,
∴AE=ABsinB=3![]() sin45°=3
sin45°=3![]() ×
×![]() =3,
=3,
∵∠B=45°,∴∠BAE=45°,∴BE=AE=3,
在Rt△ACE中,
∵tan∠ACB=![]() ,
,
∴EC=![]() ,
,
∴BC=BE+EC=3+![]() ;
;
(2)连接AO并延长到⊙O上一点M,连接CM,
由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=![]() ,
,
∴AC=2![]() ,
,
∵∠D=∠M=60°,
∴sin60°=![]() ,
,
解得:AM=4,
∴⊙O的半径为2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目