Question

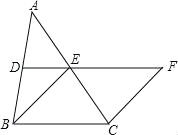
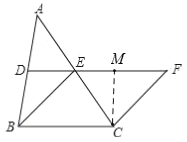
【题目】如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF．

（1）求证：四边形BCFE是菱形；

（2）若CE＝2，∠BCF＝120°，求菱形BCFE的面积．

Answer 1

【答案】（1）见解析；（2）2

【解析】

(1)根据菱形定义“一组邻边相等的平行四边形是菱形”，先证明四边形的对边平行，然后再证明邻边相等即可；

(2)过点C作CM⊥EF，垂足为M，由已知可证得△ECF是等边三角形，继而求得CM的长，然后利用菱形面积公式进行求解即可.

(1)∵D、E分别是AB、AC的中点，

∴DE∥BC，BC＝2DE，

∵EF＝BE，BE＝2DE，

∴EF＝BC＝BE，EF∥BC，

∴四边形BCFE是平行四边形，

∵BE＝BC，

∴四边形BCFE是菱形．

(2)过点C作CM⊥EF，垂足为M，则∠CMF=90°，

∵EF∥BC，

∴∠EFC+∠BCF＝180°，

∵∠BCF＝120°，

∴∠EFC＝60°，

∵FE＝FC，

∴△ECF是等边三角形，

∴EF=FC=CE=2，

又∵CM⊥EF，

∴∠FCM=30°，

∴FM=CF=1，

∴CM==，

∴S菱形BCFE＝EFCM＝2．