题目内容
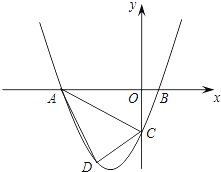
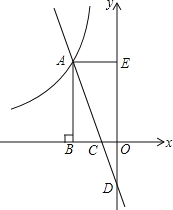
【题目】如图,直线y=kx﹣2与双曲线y=-![]() (x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(1)直接写出四边形OCAE的面积;
(2)求点C的坐标.
【答案】(1)四边形OCAE的面积为4;(2)C(﹣![]() ,0).
,0).
【解析】(1)根据反比例函数系数k的几何意义即可求得;(2)设A(x,-![]() ),根据△ABC的面积为2,求得BC= -
),根据△ABC的面积为2,求得BC= -![]() x,OC=-
x,OC=-![]() x,根据△ABC∽△DOC求得
x,根据△ABC∽△DOC求得![]() ,由直线的解析式求得D的坐标为(0,-2)得出OD=2,从而求得AB=4,代入反比例函数解析式求得A的坐标,求得OB的长,即可求得C的坐标.
,由直线的解析式求得D的坐标为(0,-2)得出OD=2,从而求得AB=4,代入反比例函数解析式求得A的坐标,求得OB的长,即可求得C的坐标.
(1)∵双曲线为y=﹣![]() (x<0),
(x<0),
∴四边形ABOE的面积为6,
∵△ABC的面积为2.
∴四边形OCAE的面积为4.
(2)∵A点是双曲线y=﹣![]() (x<0)上的点,
(x<0)上的点,
设A(x,﹣![]() ),
),
∴AB=﹣![]() ,
,
∵△ABC的面积为2.
∴![]() ABBC=2,即
ABBC=2,即![]() ×(﹣
×(﹣![]() )BC=2
)BC=2
∴BC=﹣![]() x,
x,
∴OC=﹣![]() x,
x,
∵AB⊥x轴于点B,
∴AB∥y轴,
∴△ABC∽△DOC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
由直线y=kx﹣2可知D(0,﹣2),
∴OD=2,
∴AB=4,
∴﹣![]() =4,解得x=﹣
=4,解得x=﹣![]() ,
,
∴A(﹣![]() ,4),
,4),
代入![]() k﹣2,解得k=﹣4,
k﹣2,解得k=﹣4,
∴直线:y=﹣4x﹣2,
令y=0,则x=﹣![]() ,
,
∴C(﹣![]() ,0).
,0).

 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?