题目内容
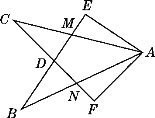
【题目】如图,在正方形ABCD中,OE=OF.求证:△AOE≌△BOF,AE⊥BF. 
【答案】证明:∵四边形ABCD为正方形, ∴OA=OB,∠AOE=∠BOF;
在△AOE与△BOF中,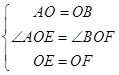 ,
,
∴△AOE≌△BOF(SAS),
延长AE交BF于点G;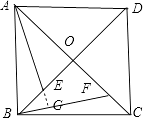
∵△AOE≌△BOF,
∴∠AEO=∠OFG,即∠AEO=∠AFG.
∵AO⊥EO,
∴∠EAO+∠AEO=90°,
∴∠GAF+∠AFG=90°,
∴AE⊥BF.
∴△AOE≌△BOF,AE⊥BF.
【解析】利用正方形的性质可得AO=BO,∠AOE=∠BOF,又OE=OF,可证明△AOE≌△BOF,得到AE=BF,延长AE交BF于点G,证明∠AEO=∠AFG.证明∠GAF+∠AFG=90°,即可解决问题.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目