Question

【题目】如图，一次函数y=kx+b的图像与反比例函数y= （x＞0）的图像交于点P（n，2），与x轴交于点A（﹣4，0），与y轴交于点C，PB⊥x轴于点B，且AC=BC．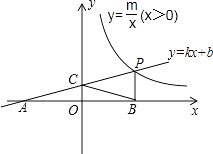

（1）求一次函数、反比例函数的解析式；
（2）反比例函数图像上是否存在点D，使四边形BCPD为菱形？如果存在，求出点D的坐标；如果不存在，说明理由．

Answer 1

【答案】
（1）

解：∵AC=BC，CO⊥AB，A（﹣4，0），

∴O为AB的中点，即OA=OB=4，

∴P（4，2），B（4，0），

将A（﹣4，0）与P（4，2）代入y=kx+b得： ，

解得：k= ，b=1，

∴一次函数解析式为y= x+1，

将P（4，2）代入反比例解析式得：m=8，即反比例解析式为y=

（2）

解：假设存在这样的D点，使四边形BCPD为菱形，如图所示，连接DC与PB交于E，

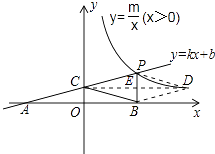
∵四边形BCPD为菱形，

∴CE=DE=4，

∴CD=8，

将x=8代入反比例函数y= 得y=1，

∴D点的坐标为（8，1）

∴则反比例函数图像上存在点D，使四边形BCPD为菱形，此时D坐标为（8，1）．

【解析】（1）由AC=BC，且OC⊥AB，利用三线合一得到O为AB中点，求出OB的长，确定出B坐标，从而得到P点坐标，将P与A坐标代入一次函数解析式求出k与b的值，确定出一次函数解析式，将P坐标代入反比例解析式求出m的值，即可确定出反比例解析式；（2）假设存在这样的D点，使四边形BCPD为菱形，根据菱形的特点得出D点的坐标．
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远才能正确解答此题．