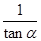题目内容
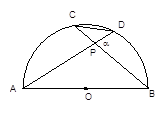
【初始问题】如图1,已知两个同心圆,直线AD分别交大⊙O于点A、D,交小⊙O于点B、C.AB与CD相等吗?请证明你的结论.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).
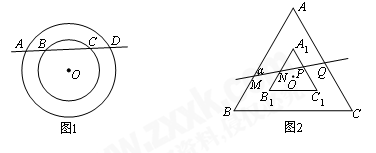
小题1:(1)求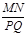 (用含∠α的式子表示);
(用含∠α的式子表示);
小题2:(2)求∠α等于多少度时,MN = PQ.
【类比研究】如图2,若两个等边三角形ABC和A1 B1 C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与A1B1,BC与B1C1,AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q,与AB所成夹角为∠α(30°<∠α<90°).

小题1:(1)求
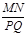 (用含∠α的式子表示);
(用含∠α的式子表示);小题2:(2)求∠α等于多少度时,MN = PQ.
小题1:解:【初始问题】结论:AB = CD. ……………………… 1分
证明:如图,作OE⊥AD于E.
∴ AE=ED,BE=EC. …………………………………………… 2分
∴ AE-BE=ED-EC.
即AB=CD. ……………………………………………………… 3分
【类比研究】(1)如图,作ND⊥AB于D,PE⊥AC于E. ……… 4分
则ND=PE.
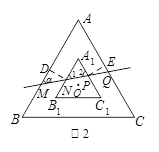 ∵AB∥A1B1,
∵AB∥A1B1,∴ ∠1=∠α.
∵等边三角形A1 B1 C1中,∠A1=60°,
∴ ∠2=120°-∠1=120°-∠α.
∵AC∥A1C1,
∴ ∠PQE=∠2=120°-∠α.
∵30°<∠α<90°,
∴ 30°<120°-∠α<90°.
∴ 在Rt△MDN和Rt△QEP中,
DN=MN
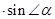 ,PE
,PE = PQ
= PQ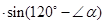 . …………………… 6分
. …………………… 6分∴MN
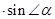 = PQ
= PQ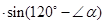 .
.∴
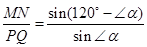 .
. 小题2:(2)当120°-∠α =∠α时,即∠α = 60°时,MN=PQ.
略

练习册系列答案
相关题目
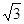 ,某物体沿斜面向上推进了10米,那么物体升高了 米.
,某物体沿斜面向上推进了10米,那么物体升高了 米. -
-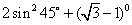
 ,tan∠ADC=2.
,tan∠ADC=2.
 方向平移得到
方向平移得到 .如果
.如果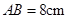 ,
,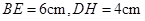 ,则图中阴影部分面积为
,则图中阴影部分面积为 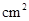 .
.
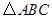 中,
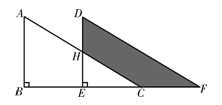
中,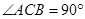 ,点D是斜边AB上的一点,且CD=AC=3,AB=4,求
,点D是斜边AB上的一点,且CD=AC=3,AB=4,求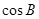 ,
,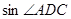 及
及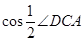 的值.
的值.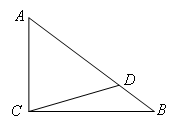
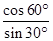 -tan45°+sin245°.
-tan45°+sin245°.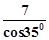
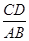 等于( )
等于( )