题目内容
(本小题满分6分)
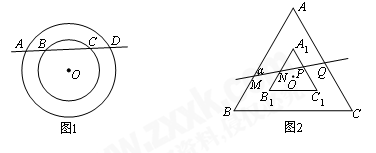
如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD= ,tan∠ADC=2.
,tan∠ADC=2.

小题1:(1)求证:CD是半圆O的切线
小题2:(2)求半圆O的直径;
小题3:(3)求AD的长.
如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=
 ,tan∠ADC=2.
,tan∠ADC=2.
小题1:(1)求证:CD是半圆O的切线
小题2:(2)求半圆O的直径;
小题3:(3)求AD的长.
小题1:
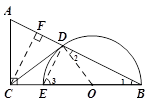 (1)证明:如图,连接OD,
(1)证明:如图,连接OD,∵OD=OB,∴∠1=∠2.
∵CA=CD,∴∠ADC=∠A.
在△ABC中,
∵∠ACB=90°,∴∠A+∠1=90°.
∴∠ADC+∠2=90°. ∴∠CDO=90°.
∵OD为半圆O的半径,
∴CD为半圆O的切线.
小题2:(2)解:如图,连接DE.
∵BE为半圆O的直径,
∴∠EDB=90°.∴∠1+∠3=90°.
∴∠
 ADC=∠3.
ADC=∠3.∴
 .
.∴
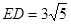 .
.∴
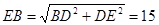 .
.小题3:(3)解:作CF⊥AD于点F,∴AF=DF.
设
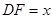 ,
,∵
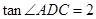 ,∴CF=2x.
,∴CF=2x.∵∠1+∠FCB=90°,
∴
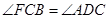 .
.∴
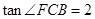 . ∴FB=4x.
. ∴FB=4x. ∴BD=3 x=
 . 解得
. 解得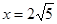 .
.∴AD=2DF=2x=
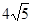
略

练习册系列答案
相关题目
 的度数(精确到1º)
的度数(精确到1º)
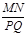 (用含∠α的式子表示);
(用含∠α的式子表示); 中,斜边
中,斜边 的长为
的长为 ,
, ,则直角边
,则直角边 的长是( )
的长是( )




 中,
中, ,则
,则

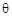 ,一般情况下,倾角
,一般情况下,倾角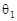 减至
减至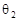 ,这样楼梯占用地板的长度
,这样楼梯占用地板的长度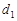 增加到
增加到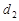 ,已知
,已知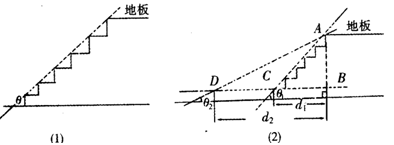
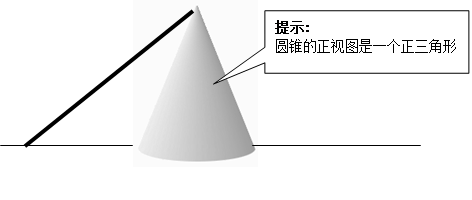
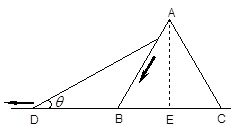
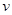 (木棒下滑为匀速)已知木棒与水平地面的夹角为
(木棒下滑为匀速)已知木棒与水平地面的夹角为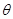 ,
,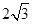
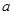 。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度
。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度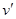 为多少?
为多少? ,B地的俯角为
,B地的俯角为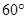 (点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.
(点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.