Question

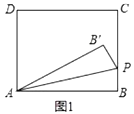
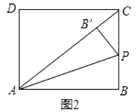
【题目】如图，在菱形中，，，点是边的中点，点是边上一动点（不与点重合），延长交射线于点，连接，．

（1）求证：四边形是平行四边形；

（2）填空：

①当的值为_______时，四边形是矩形；

②当的值为______时，四边形是菱形．

Answer 1

【答案】（1）见解析；（2）①3，②6

【解析】

（1）根据菱形的性质得出，再利用平行线的性质以及线段中点的性质得出，即可得出答案；

（2）①由∠AMD=90°，根据含30度直角三角形的性质即可得出答案；②判定△AMD是等边三角形即可得出答案．

解：（1）证明：∵四边形是菱形，

∴，∴，

∵点是边的中点，∴，

在和中，

∴，

∴，

∴四边形是平行四边形；

（2）①当的值为3时，四边形是矩形．

当四边形是矩形时，∠AMD=90°，

∵∠DAM=60°，AD=AB=6，

∴AM＝3；

②当的值为6时，四边形是菱形．

当四边形是菱形时，MA＝MD，

∵∠DAM=60°，

∴△AMD是等边三角形，

∴AM=AD=6．