题目内容
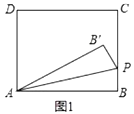
【题目】如图，一副三角板
和
拼合在一起，边
与
重合，
，
，
，
．当点
从点
出发沿向下滑动时，点
同时从点
出发沿射线
向右滑动．当点从点滑动到点时，连接
，则
的面积最大值为_______
．
【答案】
【解析】
根据勾股定理分别求出BC和FD的长度，再根据题意得出点D到BC的最大距离为DF，计算即可得出答案．
在Rt△ABC中，∠BAC=30°，∠ACB=90°，AC=6cm
可设CB=xcm，AB=2xcm
根据勾股定理可得
∴BC=2
cm
在Rt△EDF中，∠EDF=90°，∠DEF=45°，EF=AC=6cm
可设ED=FD=ycm
可得
∴DF=ED=3
cm
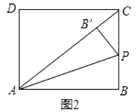
在点F从点C出发沿射线BC向右滑动的过程中，当DF⊥BC时，点D到BC的距离最大最大值为DF，
此时
，
故答案为．
练习册系列答案
相关题目
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
（1）根据表格中的数据，确定b，c，n的值；
（2）设y=﹣x2+bx+c，直接写出0≤x≤2时y的最大值.
