题目内容
如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(-
,
)].
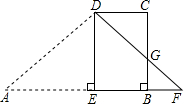
(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
[参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |

(1)由题意,得EF=AE=DE=BC=x,AB=30,
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF=∠ABC=90°,
∴∠BGF=∠F=45°.
∴BG=BF=2x-30,
∴S=S△DEF-S△GBF=
DE2-
BF2
=
x2-
(2x-30)2
=-
x2+60x-450.
(3)S=-
x2+60x-450=-
(x-20)2+150.
∵a=-
<0,15<20<30,
∴当x=20时,S有最大值,最大值为150
∴BF=2x-30.
(2)∵∠F=∠A=45°,∠CBF=∠ABC=90°,
∴∠BGF=∠F=45°.
∴BG=BF=2x-30,
∴S=S△DEF-S△GBF=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
(3)S=-
| 3 |
| 2 |
| 3 |
| 2 |
∵a=-
| 3 |
| 2 |
∴当x=20时,S有最大值,最大值为150

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目