题目内容
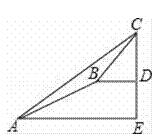
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
【答案】8.1米
【解析】试题分析:作BF⊥AE于F,则FE=BD=6米,DE=BF,设BF=x米,则AF=2.4米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=5米,AF=12米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
试题解析:解:作BF⊥AE于F,如图所示,则FE=BD=6米,DE=BF.∵斜面AB的坡度i=1:2.4,∴AF=2.4BF.设BF=x米,则AF=2.4x米.在Rt△ABF中,由勾股定理得: ![]() ,解得:x=5,∴DE=BF=5米,AF=12米,∴AE=AF+FE=18米.在Rt△ACE中,CE=AEtan36°=18×0.73=13.14米,∴CD=CE﹣DE=13.14米﹣5米≈8.1米.
,解得:x=5,∴DE=BF=5米,AF=12米,∴AE=AF+FE=18米.在Rt△ACE中,CE=AEtan36°=18×0.73=13.14米,∴CD=CE﹣DE=13.14米﹣5米≈8.1米.

答:大树CD的高度约为8.1米.

【题目】为弘扬“雷锋精神”,我县开展“做雷锋精神种子.当四品八德少年”主题征文比赛,已知每篇参赛征文成绩记![]() 分(
分(![]() ) ,组委会从
) ,组委会从![]() 篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
县主题征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
县主题征文比赛成绩频数分布直方图
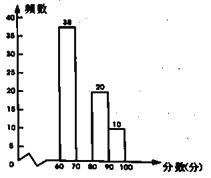
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图:
(3)若![]() 分以上(含
分以上(含![]() 分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.