题目内容
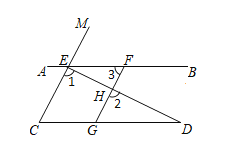
【题目】已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
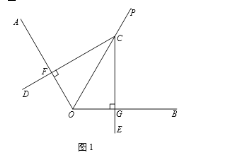
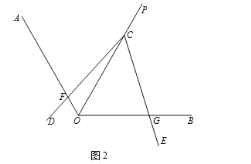
【答案】(1)CF=CG;(2)CF=CG,见解析
【解析】
(1)结论CF=CG,由角平分线性质定理即可判断.
(2)结论:CF=CG,作CM⊥OA于M,CN⊥OB于N,证明△CMF≌△CNG,利用全等三角形的性质即可解决问题.
解:(1)结论:CF=CG;
证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,
∴CF=CG(角平分线上的点到角两边的距离相等);
(2)CF=CG.理由如下:如图,
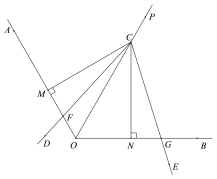
过点C作CM⊥OA,CN⊥OB,
∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120,
∴CM=CN(角平分线上的点到角两边的距离相等),
∴∠AOC=∠BOC=60(角平分线的性质),
∵∠DCE=∠AOC,
∴∠AOC=∠BOC=∠DCE=60,
∴∠MCO=90-60 =30,∠NCO=90-60 =30,
∴∠MCN=30+30=60,
∴∠MCN=∠DCE,
∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,
∴∠MCF=∠NCG,
在△MCF和△NCG中,
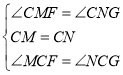
∴△MCF≌△NCG(ASA),
∴CF=CG(全等三角形对应边相等);

 阅读快车系列答案
阅读快车系列答案【题目】公园里有一人设了个游戏摊位,游客只需掷一枚正方体骰子,如果出现3点,就可获得价值10元的奖品,每抛掷1次骰子只需付1元的费用.小明在摊位前观察了很久,记下了游客的中奖情况:
游客 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
抛掷次数 | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
中奖次数 | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
看了小明的记录,你有什么看法?