题目内容
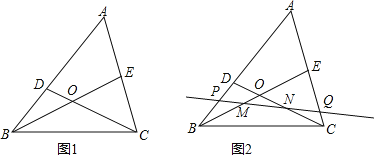
【题目】如图,在![]() 中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且
中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且![]() .
.
![]() 求证:
求证: ![]() ∽
∽![]() ;
;
![]() 求证:
求证: ![]() ;
;
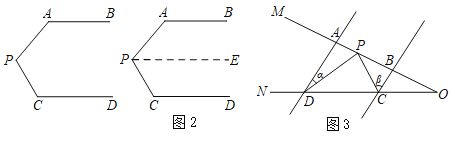
![]() 若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
【答案】(1)证明见解析;(2)证明见解析;(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)根据已知条件得到∠DOB=∠A,由于∠ABE=∠ABE,于是得到结论;
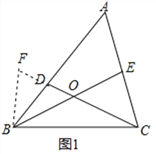
(2)延长CD,在CD延长线上取一点F,使BF=BD,根据等腰三角形的性质得到∠BDF=∠BFD,根据三角形的外角的性质得到∠BDF=∠BEC,于是得到∠BFD=∠BEC,根据全等三角形的性质即可得到结论;
(3)取BC的中点G,连接GM,GN,根据三角形中位线的性质得到GM∥CE,GM=![]() CE,GN∥BD,GN=
CE,GN∥BD,GN=![]() BD,根据平行线的性质得到∠2=∠4,∠3=∠1,等量代换得到∠1=∠2,于是得到AP=AQ.
BD,根据平行线的性质得到∠2=∠4,∠3=∠1,等量代换得到∠1=∠2,于是得到AP=AQ.
试题解析: ![]() 证明:
证明: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ;
;
![]() 解:延长CD,在CD延长线上取一点F,使
解:延长CD,在CD延长线上取一点F,使![]() ,
,
![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中, 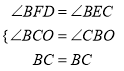 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ;
;
![]() 解:
解: ![]() ,
,

理由:取BC的中点G,连接![]() ,
,
![]() 分别是
分别是![]() 的中点,
的中点,
![]() 是中位线,
是中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目