ƒøƒĞ»ı
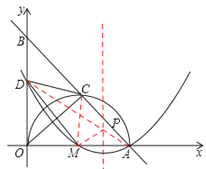
°æƒø°ø»ÁÕº£¨‘Ğ÷±Ω«ÃÂœµ÷–£¨÷±œşABΩªx÷·”е„A£®5£¨0£©£¨Ωªy÷·”е„B£¨AO «°—Mµƒ÷±æ∂£¨∆‰∞Α≤ΩªAB”е„C£¨«“AC=3°£»°BOµƒ÷–µ„D£¨¡¨Ω”CD°¢MD∫ÕOC°£

£®1£©«Û÷§£∫CD «°—Mµƒ«–œş£ª
£®2£©∂˛¥Œ∫Ø ˝µƒÕºœÛæ≠π˝µ„D°¢M°¢A£¨∆‰∂‘≥∆÷·…œ”–“ª∂ص„P£¨¡¨Ω”PD°¢PM£¨«Û°˜PDMµƒ÷İ≥§◊Ó–° ±µ„Pµƒ◊¯±Í£ª
£®3£©‘Ğ£®2£©µƒÃº˛œ¬£¨µ±°˜PDMµƒ÷İ≥§◊Ó–° ±£¨≈◊ŒÔœş…œ «∑ҥʑе„Q£¨ π![]() £ø»Ù¥Ê‘Ğ£¨«Û≥ˆµ„Qµƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…°£
£ø»Ù¥Ê‘Ğ£¨«Û≥ˆµ„Qµƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…°£
°æ¥∞∏°øΩ‚£∫£®1£©÷§√˜£∫¡¨Ω”CM£¨
°şOA Œ™°—M÷±æ∂£¨°‡°œOCA=90°„°£°‡°œOCB=90°„°£
°şDŒ™OB÷–µ„£¨°‡DC=DO°£°‡°œDCO=°œDOC°£
°şMO=MC£¨°‡°œMCO=°œMOC°£
°‡![]() °£
°£
”÷°şµ„C‘Ğ°—M…œ£¨°‡DC «°—Mµƒ«–œş°£
£®2£©°şAµ„◊¯±Í£®5£¨0£©£¨AC=3
°‡‘ĞRt°˜ACO÷–£¨![]() °£
°£
°‡![]() £¨°‡
£¨°‡![]() £¨Ω‚µ√
£¨Ω‚µ√ ![]() °£
°£
”÷°şDŒ™OB÷–µ„£¨°‡![]() °£°‡Dµ„◊¯±ÍŒ™£®0£¨
°£°‡Dµ„◊¯±ÍŒ™£®0£¨![]() )°£
)°£
¡¨Ω”AD£¨…Ë÷±œşADµƒΩ‚Œˆ ΩŒ™y=kx+b£¨‘Ú”–
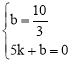 Ω‚µ√
Ω‚µ√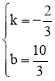 °£
°£
°‡÷±œşADŒ™![]() °£
°£
°ş∂˛¥Œ∫Ø ˝µƒÕºœÛπ˝M£®![]() £¨0)°¢A(5£¨0)£¨
£¨0)°¢A(5£¨0)£¨
°‡≈◊ŒÔœş∂‘≥∆÷·x=![]() °£
°£
°şµ„M°¢Aπÿ”Ğ÷±œşx=![]() ∂‘≥∆£¨…Ë÷±œşAD”Î÷±œşx=
∂‘≥∆£¨…Ë÷±œşAD”Î÷±œşx=![]() Ωª”е„P£¨
Ωª”е„P£¨
°‡PD+PMŒ™◊Ó–°°£
”÷°şDMŒ™∂®≥§£¨°‡¬˙◊„ú˛µƒµ„PŒ™÷±œşAD”Î÷±œşx=![]() µƒΩªµ„°£
µƒΩªµ„°£
µ±x=![]() ±£¨
±£¨![]() °£
°£
°‡Pµ„µƒ◊¯±ÍŒ™£®![]() £¨
£¨![]() £©°£
£©°£
£®3£©¥Ê‘Ğ°£
°ş![]() £¨
£¨![]()
”÷”…£®2£©÷™D£®0£¨![]() )£¨P£®
)£¨P£®![]() £¨
£¨![]() £©£¨
£©£¨
°‡”…![]() £¨µ√
£¨µ√![]() £¨Ω‚µ√yQ=°¿
£¨Ω‚µ√yQ=°¿![]() °£
°£
°ş∂˛¥Œ∫Ø ˝µƒÕºœÒπ˝M(0£¨![]() )°¢A(5£¨0£©£¨
)°¢A(5£¨0£©£¨
°‡…Ë∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™![]() £¨
£¨
”÷°ş∏√ÕºœÛπ˝µ„D£®0£¨![]() )£¨°‡
)£¨°‡![]() £¨Ω‚µ√a=
£¨Ω‚µ√a=![]() °£
°£
°‡∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™![]() °£
°£
”÷°şQµ„‘Ğ≈◊ŒÔœş…œ£¨«“yQ=°¿![]() °£
°£
°‡µ±yQ=![]() ±£¨
±£¨![]() £¨Ω‚µ√x=
£¨Ω‚µ√x=![]() ªÚx=
ªÚx=![]() £ª
£ª
µ±yQ=![]() ±£¨
±£¨![]() £¨Ω‚µ√x=
£¨Ω‚µ√x=![]() °£
°£
°‡µ„Qµƒ◊¯±ÍŒ™£®![]() £¨
£¨![]() )£¨ªÚ£®
)£¨ªÚ£®![]() £¨
£¨![]() )£¨ªÚ£®
)£¨ªÚ£®![]() £¨
£¨![]() £©°£
£©°£
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©¡¨Ω”CM£¨ø…“‘µ√≥ˆCM=OM£¨æÕ”–°œMOC=°œMCO£¨”…OAŒ™÷±æ∂£¨æÕ”–°œACO=90°„£¨DŒ™OBµƒ÷–µ„£¨æÕ”–CD=OD£¨°œDOC=°œDCO£¨”…°œDOC+°œMOC=90°„æÕø…“‘µ√≥ˆ°œDCO+°œMCO=90°„∂¯µ√≥ˆΩ·¬ğ°£
£®2£©∏˘æıú˛ø…“‘µ√≥ˆ![]() ∫Õ
∫Õ![]() £¨¥”∂¯«Û≥ˆOBµƒ÷µ£¨∏˘æıD «OBµƒ÷–µ„æÕø…“‘«Û≥ˆDµƒ◊¯±Í£¨”…¥˝∂®œµ ˝∑®æÕø…“‘«Û≥ˆ≈◊ŒÔœşµƒΩ‚Œˆ Ω£¨«Û≥ˆ∂‘≥∆÷·£¨∏˘æı÷·∂‘≥∆µƒ–‘÷ ¡¨Ω”ADΩª∂‘≥∆÷·”ĞP£¨œ»«Û≥ˆADµƒΩ‚Œˆ ΩæÕø…“‘«Û≥ˆPµƒ◊¯±Í°£
£¨¥”∂¯«Û≥ˆOBµƒ÷µ£¨∏˘æıD «OBµƒ÷–µ„æÕø…“‘«Û≥ˆDµƒ◊¯±Í£¨”…¥˝∂®œµ ˝∑®æÕø…“‘«Û≥ˆ≈◊ŒÔœşµƒΩ‚Œˆ Ω£¨«Û≥ˆ∂‘≥∆÷·£¨∏˘æı÷·∂‘≥∆µƒ–‘÷ ¡¨Ω”ADΩª∂‘≥∆÷·”ĞP£¨œ»«Û≥ˆADµƒΩ‚Œˆ ΩæÕø…“‘«Û≥ˆPµƒ◊¯±Í°£
£®3£©∏˘æı![]() £¨
£¨![]() «Û≥ˆQµƒ◊ı◊¯±Í£¨«Û≥ˆ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ωº¥ø…«Ûµ√∫·◊¯±Í°£
«Û≥ˆQµƒ◊ı◊¯±Í£¨«Û≥ˆ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ωº¥ø…«Ûµ√∫·◊¯±Í°£

 —ß“µ≤‚∆¿“ªøŒ“ª≤‚œµ¡–¥∞∏
—ß“µ≤‚∆¿“ªøŒ“ª≤‚œµ¡–¥∞∏ –°—ßøŒ ±◊˜“µ»´Õ®¡∑∞∏œµ¡–¥∞∏
–°—ßøŒ ±◊˜“µ»´Õ®¡∑∞∏œµ¡–¥∞∏°æƒø°øƒ≥ÀÆπ˚µÍ¬Ù≥ˆµƒœ„Ω∂ ˝¡ø£®«ßøÀ£©”Î ğºğ£®‘™£©÷ƺ‰µƒπÿœµ»Á±Ì£∫
˝¡ø£®«ßøÀ£© | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | °≠ |
ğºğ£®‘™£© | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | °≠ |
…œ±Ì∑¥”≥¡À∏ˆ±‰¡ø÷ƺ‰µƒπÿœµ£¨∆‰÷–£¨◊‘±‰¡ø «£ª“Ú±‰¡ø « £Æ

