Question

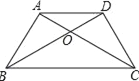
【题目】如图，已知梯形ABCD中，AD∥BC，AB=CD=AD，AC、BD相交于点O，∠BCD=60°，则下列4个结论：①梯形ABCD是轴对称图形；②BC=2AD；③梯形ABCD是中心对称图形；④AC平分∠DCB，其中正确的是_____．

Answer 1

【答案】①②④

【解析】

根据等腰梯形的性质即可求出答案．

①∵AB=CD，

∴梯形ABCD是等腰梯形，

∴过点O作直线l⊥BC，此时直线l为梯形的对角线，故①正确；

②如图，过点D作DE∥AB，

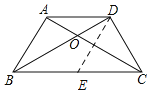
易证，四边形ADEB是平行四边形，

∴AD=BE，AB=DE，

∵AB=CD，

∴DE=CD，

∵∠BCD=60°，

∴△DEC是等边三角形，

∴CE=CD，

∴BC=BE+CE=AD+CD=2AD，故②正确；

③根据中心对称图形的定义可知等腰梯形ABCD不是中心对称图形，故③错误；

④∵AD=CD，

∴∠DAC=∠DCA，

∵AD∥BC，

∴∠DAC=∠ACB，

∴∠DCA=∠ACB，

∴CA平分∠DCB，故④正确；

故答案为：①②④