题目内容
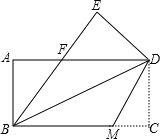
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形式菱形,理由见解析.
【解析】试题分析:(1)因为△BCD关于BD折叠得到△BED,显然△BCD≌△BED,得出CD=DE=AB,∠E=∠C=∠A=90°.再加上一对对顶角相等,可证出△ABF≌△EDF
(2)利用折叠知识及菱形的判定可得出四边形BMDF是菱形.
试题解析:(1)由折叠可知,CD=ED,∠E=∠C.
在矩形ABCD中,AB=CD,∠A=∠C.
∴AB=ED,∠A=∠E.
∵∠AFB=∠EFD,
∴△AFB≌△EFD.
(2)四边形BMDF是菱形.
理由:由折叠可知:BF=BM,DF=DM.
由(1)知△AFB≌△EFD,
∴BF=DF.
∴BM=BF=DF=DM.
∴四边形BMDF是菱形.

练习册系列答案
相关题目