题目内容
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
![]() 当点
当点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
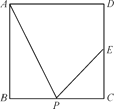
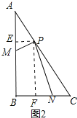
、![]() 上时(如图
上时(如图![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,请探索
,请探索![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 当
当![]() ,
,
①点![]() 、
、![]() 分别在线段
分别在线段![]() 、
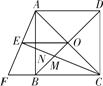
、![]() 上,如图
上,如图![]() 时,请写出线段
时,请写出线段![]() 、
、![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
②当点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 的延长线上,如图
的延长线上,如图![]() 时,请判断①中线段
时,请判断①中线段![]() 、
、![]() 之间的数量关系是否还存在.(直接写出答案,不用证明)
之间的数量关系是否还存在.(直接写出答案,不用证明)

【答案】(1)![]() ,理由见解析;
,理由见解析;![]() ①
①![]() ,理由见解析;②成立.
,理由见解析;②成立.
【解析】
(1)过点P作PE⊥AB于E,PF⊥BC于点F,则四边形BFPE是矩形,所以△PFN∽△PEM得出![]() ,然后根据余切函数即可求得.
,然后根据余切函数即可求得.
(2)同(1)证得△PFN∽△PEM得出![]() ,然后在Rt△AEP和Rt△PFC中通过三角函数求得PF=
,然后在Rt△AEP和Rt△PFC中通过三角函数求得PF=![]() PC,PE=
PC,PE=![]() PA,即可求得.
PA,即可求得.
(1)![]() ,
,
理由:如图![]() ,作
,作![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]()
∴![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
即![]() .
.
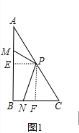
![]() ,
,
如图![]() 在
在![]() 中,过点
中,过点![]() 于点
于点![]()
∴四边形![]() 是矩形,
是矩形,
∴![]()
∴![]() ,
,
又∵![]() 中,
中,![]()
∴![]()
∴![]()
∵![]()
∴![]() ,
,
即:![]()
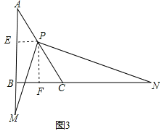
②如图![]() ,成立.
,成立.

练习册系列答案
相关题目