题目内容
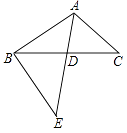
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.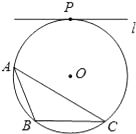
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.
【答案】
(1)解:如图所示:
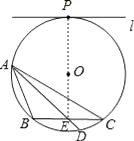
(2)解:∵直线l与⊙O相切与点P,∴OP⊥l,∵l∥BC,∴PE⊥BC,
∴BE=CE,∴弦AE将△ABC分成面积相等的两部分.
【解析】(1)根据垂径定理作PE⊥BC于E即可得答案;
(2)利用根据垂径定理可知BE=CE,即E为BC中点,再由三角形的中线把三角形分成面积相等的两部分可得出结论.
【考点精析】根据题目的已知条件,利用三角形的“三线”和垂径定理的相关知识可以得到问题的答案,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目