题目内容
【题目】如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
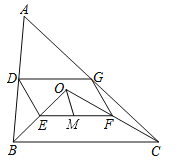
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
【答案】（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=
BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，∴DG∥BC，DG=BC，∵E、F分别是OB、OC的中点，∴EF∥BC，EF=BC，∴DE=EF，DG∥EF，∴四边形DEFG是平行四边形；
（2）∵∠OBC和∠OCB互余，∴∠OBC+∠OCB=90°，∴∠BOC=90°，∵M为EF的中点，OM=3，∴EF=2OM=6．
由（1）有四边形DEFG是平行四边形，∴DG=EF=6．
【题目】为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．如表是该市居民“一户一表”生活用水及提示计费价格表的部分信息：（说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费用）
已知小王家2012年4月份用水20吨，交水费66元；5月份用水25吨，交水费91元．
（1）求a、b的值；
（2）随着夏天的到来，用水量将增加．为了节省开支，小王计划把6月份的水费控制在不超过家庭月收入的2%．若小王家的月收入为9200元，则小王家6月份最多能用水多少吨？
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价：元/吨 | 单价：元/吨 |
17吨以下 | a | 0.80 |
超过17吨但不超过30吨部分 | b | 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
