题目内容
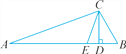
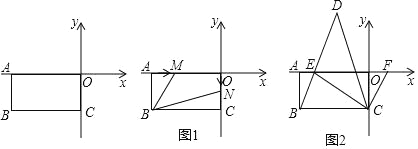
【题目】我们做个折纸游戏：第一步：在一张矩形纸片的一端，利用图
的方法折出一个正方形，然后把纸片展开；第二步：如图
，把这个正方形折成两个相等的矩形，再把纸片展开；第三步：折出内侧矩形的对角线
，并把它折到图
中所示的
处；第四步：如图
， 展平纸片，按照所得的
点折出
．则矩形
的宽
与长
的比是__________．
【答案】
【解析】
设正方形的边长为2a，由折叠的性质，可得AC＝正方形的边长×
＝a，在Rt△ABC中，利用勾股定理可求出AB与正方形的边长之间的关系，再求出CD＝
aa，即可求解．
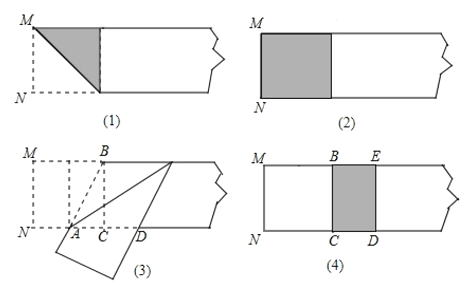
在正方形BCNM中，令NC＝2a，∴BC=NC=2a，
∵A为NC的中点，
∴AC＝NC＝a．
在Rt△ABC中，AB＝
=a．
又∵AD＝AB，
∴CD＝ADAC＝（1）a．
∴矩形BCDE的宽CD与长BC的比＝
故答案为：．
练习册系列答案
相关题目
