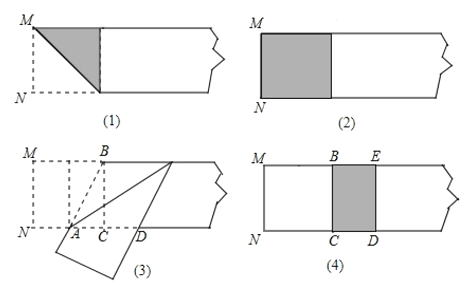
��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�A(a��0)��C(0��c)�����㣺(a+6)2+![]() ��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮
��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮
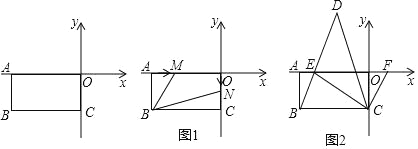
(1)���B�����꣮
(2)��ͼ1������M�ӵ�A��������2����λ/����ٶ������˶�(��������O)����N��ԭ��O��������1����λ/����ٶ������˶�(��������C)����M��N����ͬʱ�������������˶��Ĺ����У��ı���MBNO������Ƿ����仯�������䣬����ֵ�����仯����仯�ķ�Χ��
(3)��ͼ2��EΪx�Ḻ������һ�㣬�ҡ�CBE����CEB��F��x����������һ���㣬��ECF��ƽ����CD��BE���ӳ����ڵ�D���ڵ�F�˶��Ĺ����У���̽����CFE���D��������ϵ����˵������
���𰸡�(1)B(��6����3)��(2)�ı���MBNO��������䣻�Ƕ�ֵ9��(3)��CFE��2��D.
��������
��1����������ɵ�a����6��c����3�������A�㣬C�㣬B�����ꣻ��2����M��Nͬʱ������ʱ��Ϊt����S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
�⣺(1)��(a+6)2+![]() ��0��
��0��
��a����6��c����3
��A(��6��0)��C(0����3)
���ı���OABC�Ǿ���
��AO��BC��AB��OC��AB��OC��3��AO��BC��6
��B(��6����3)
(2)�ı���MBNO��������䣮
��M��Nͬʱ������ʱ��Ϊt��
��S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6��(3��t)��9����ʱ���أ�
��6��(3��t)��9����ʱ���أ�
�����˶�������������䣮�Ƕ�ֵ9
(3)��CFE��2��D��
�������£���ͼ
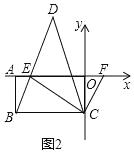
�ߡ�CBE����CEB
���ECB��180����2��BEC
��CDƽ�֡�ECF
���DCE����DCF
��AF��BC
���F��180������DCF����DCE����BCE��180����2��DCE��(180����2��BEC)
���F��2��BEC��2��DCE
�ߡ�BEC����D+��DCE
���F��2(��D+��DCE)��2��DCE
���F��2��D

 ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
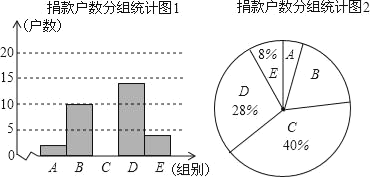
��ѧ�����ϵ�д�����Ŀ��Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͳ�Ʊ�(ͼ����Ϣ������)����֪A��B��������ı�Ϊ1��5������������Ϣ����������⣮��������ͳ�Ʊ�
��� | ����(x)Ԫ | ���� |
A | 1��x��50 | a |
B | 50��x��100 | 10 |
C | 100��x��150 | �� �� |
D | 150��x��200 | �� �� |
E | x��200 | �� �� |
(1)a���� ����������������������� ����
(2)��ȫ����������ͳ��ͼ1�;�������ͳ�Ʊ�����
(3)����������2000��ס���������������Ϣ������ȫ����������150Ԫ�Ļ�����