题目内容
【题目】已知二次函数![]() ,
,![]() 的最小值为0;
的最小值为0;![]() .当
.当![]() 时有
时有![]() ;且对于任意实数
;且对于任意实数![]() ,
,![]() .
.
(1)![]() 的对称轴为_________,顶点坐标为_____________;
的对称轴为_________,顶点坐标为_____________;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)令![]() ,试求实数
,试求实数![]() ,使得实数
,使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立.
成立.
【答案】(1)对称轴为直线![]() ,顶点坐标为
,顶点坐标为![]() (2)1(3)以当
(2)1(3)以当![]() 时使得实数
时使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立
成立
【解析】
(1)根据对称轴公式求出求出对称轴,可得顶点横坐标,根据![]() 的最小值为0可得顶点纵坐标;
的最小值为0可得顶点纵坐标;
(2)根据当![]() 时有
时有![]() 和对于任意实数
和对于任意实数![]() ,
,![]() 求解即可;
求解即可;
(3)由![]() 的最小值为0,可得
的最小值为0,可得![]() ,根据
,根据![]() 和
和![]() 求出a和b的值,然后根据二次函数的性质求解即可.
求出a和b的值,然后根据二次函数的性质求解即可.
(1)对称轴是直线x=![]() ,
,
∵![]() 的最小值为0,
的最小值为0,
∴顶点坐标为![]() ;
;
(2)∵当![]() 时有
时有![]() ,
,
∴![]() ,
,
且对任意实数![]() ,
,![]() ,
,
∴当![]() 时
时![]() ,
,
∴当![]() 时,
时,![]() ;
;
(3)由(2)得![]() ①,
①,
∵![]() 的最小值为0,
的最小值为0,
∴![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ②,
②,
由①和②解得![]() ,
,
![]()
![]() ,
,
∴![]()
![]() ,
,
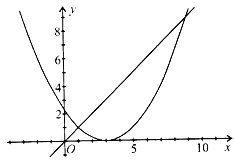
∴![]() 的图象可以看成由
的图象可以看成由![]() 左右平移而得到的,
左右平移而得到的,
根据题意当![]() 与
与![]() 图象左交点横坐标为1时,此时
图象左交点横坐标为1时,此时![]() 与
与![]() 图象右交点横坐标
图象右交点横坐标![]() 取到最大值.
取到最大值.
∴![]() ,
,
解得![]() (不合题意舍去),
(不合题意舍去),
所以当![]() 时使得实数
时使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立.
成立.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目