题目内容
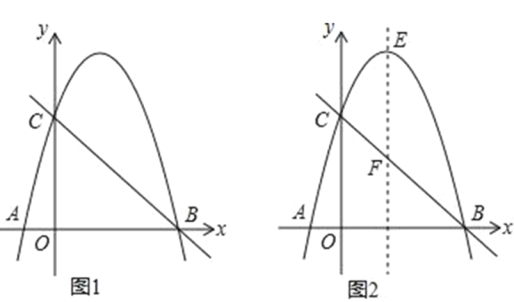
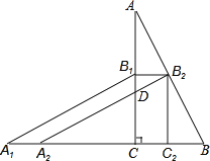
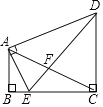
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,AB=1,AE⊥AD,交BC于点E,EA平分∠BED.
(1)CD的长是_____;
(2)当点F是AC中点时,四边形ABCD的周长是_____.
【答案】2 5+![]()
【解析】
(1)延长DA,CB交于点H,由“ASA”可证![]() ≌
≌![]() ,可得
,可得![]() ,由平行得相似,依据相似的性质即可求解;
,由平行得相似,依据相似的性质即可求解;
(2)先证明A,D,C,E四点共圆,因为F是AC中点,依据垂径定理,得到DF是AC的中垂线,依据线段的垂直平分线的性质可求得AD的长度,作![]() 于H,可证四边形ABCH是矩形,依据矩形的性质,结合线段长度,可得
于H,可证四边形ABCH是矩形,依据矩形的性质,结合线段长度,可得![]() 是
是![]() 的中垂线,由此可得AC的长度,在三角形ABC中,依据勾股定理可求得BC的长度,只需把各边相加即可得到四边形ABCD的周长.
的中垂线,由此可得AC的长度,在三角形ABC中,依据勾股定理可求得BC的长度,只需把各边相加即可得到四边形ABCD的周长.
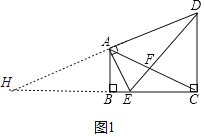
解:(1)如图1中,延长DA,CB交于点H,
∵EA平分∠BED,
∴∠AEH=∠AED,且AE=AE,∠EAH=∠EAD=90°,
∴△ADE≌△AHE(ASA)
∴AH=AD,
∵∠ABC=∠BCD=90°,
∴AB∥CD,
∴△ABH∽△DCH,
∴![]() ,且AB=1,AH=AD=
,且AB=1,AH=AD=![]() HD,
HD,
∴CD=2,
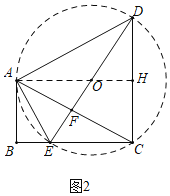
(2)如图2中,作AH⊥CD于H,
∵∠DAE=∠DCE=90°,
∴A,D,C,E四点共圆,设圆心为O,则点O是线段DE的中点,
又∵AF=CF,
∴DE⊥AC,
∴DA=DC,
∵∠ABC=∠BCH=∠AHC=90°,
∴四边形ABCH是矩形,
∴CH=AB=1,
∵CD=2,
∴CH=HD=1,
又∵AH⊥CD,
∴AD=AC,
∴AD=CD=AC=2,
∴![]() ,
,
![]() 四边形ABCD的周长为
四边形ABCD的周长为![]() .
.
故答案为:(1)2;(2)![]() .
.

练习册系列答案
相关题目