题目内容
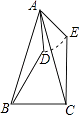
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
【答案】
(1)
解:∵抛物线顶点坐标为(1,﹣2),
∴可设抛物线解析式为y=a(x﹣1)2﹣2,
∵OA=3,且点A在x轴的正半轴上,
∴A(3,0),
∴0=a(3﹣1)2﹣2,解得a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣1)2﹣2=
(x﹣1)2﹣2= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,当x=0时可得y=﹣
,当x=0时可得y=﹣ ![]() ,
,
∴B(0,﹣ ![]() ),
),
设直线AB解析式为y=kx+b,把A、B坐标代入可得 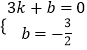 ,解得
,解得 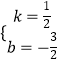 ,
,
∴y= ![]() x﹣
x﹣ ![]()
(2)
解:∵点P为线段AB上的一个动点,且PE⊥x轴,
∴点E的横坐标为x,
∵点E在抛物线上,
∴E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() )
)
(3)
解:∵点P为线段AB上的一点,
∴P(x, ![]() x﹣
x﹣ ![]() ),则E(x,
),则E(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() ),
),
∴PE= ![]() x﹣
x﹣ ![]() ﹣(
﹣( ![]() x2﹣x﹣
x2﹣x﹣ ![]() )=﹣
)=﹣ ![]() x2+
x2+ ![]() x,
x,
由(2)可知点B到PE的距离x,点A以PE的距离为3﹣x,
∴S△ABE= ![]() PEx+
PEx+ ![]() PE(3﹣x)= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/4a6d7aa9/SYS201707192035174095939404_DA/SYS201707192035174095939404_DA.001.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> PE(x+3﹣x)=
PE(3﹣x)= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/4a6d7aa9/SYS201707192035174095939404_DA/SYS201707192035174095939404_DA.001.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> PE(x+3﹣x)= ![]() PE=
PE= ![]() (﹣
(﹣ ![]() x2+
x2+ ![]() x)=﹣
x)=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当x= ![]() 时,S△ABE有最大值,最大值为
时,S△ABE有最大值,最大值为 ![]() ,
,
∴△ABE面积的最大值为 ![]()
【解析】(1)由条件可先求得抛物线解析式,则可求得B点坐标,再利用待定系数法可求得直线AB解析式;(2)由条件可知P、E的横坐标相同,又点E在抛物线上,则可表示出E点坐标;(3)由(2)可用x表示出PE的长,则可用x表示出△ABE的面积,再利用二次函数的性质可求得其最大值.