题目内容
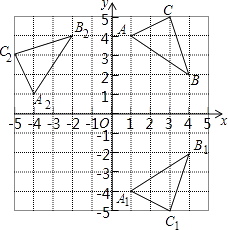
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
（1）请画出△A1B1C1 ， 使△A1B1C1与△ABC关于x轴对称；
（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2 ， 并直接写出点B旋转到点B2所经过的路径长．
【答案】
（1）
解：如图，△A1B1C1即为所求
（2）
解：如图，△A2B2C2即为所求．
点B旋转到点B2所经过的路径长为： 
= 
π．
故点B旋转到点B2所经过的路径长是 π．
【解析】（1）根据网格特点，找出点A、B、C关于x轴的对称点A1、B1、C1的位置，然后顺次连接即可；（2）分别找出点A、B、C绕点O逆时针旋转90°的对应点A2、B2、C2的位置，然后顺次连接即可，观察可知点B所经过的路线是半径为 
，圆心角是90°的扇形，然后根据弧长公式进行计算即可求解．
练习册系列答案
相关题目
